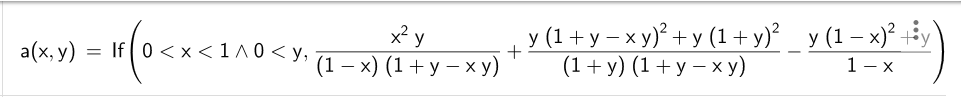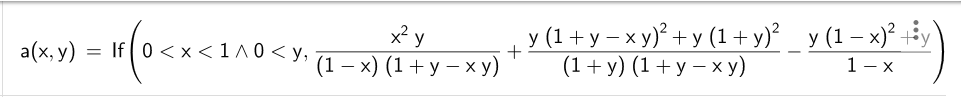Investigating trading strategies using algebra

Introduction

The other day, while I was playing around with Uniswap V2 maths, I dreamt up a possible attack. The idea was simple.

1. Swap token Y for token X
2. Add a ship-load of liquidity
3. Swap then Xs from step 1 back to token Y
4. Withdraw the liquidity from step 2

The idea behind this was that the slippage in step 3 would be much smaller than step 1 because of the added liquidity. Could this asymmetry yield an advantage?

I didn’t know.

It seemed clear that I’d make a profit on step 3 vs step 1, but this needed to be offset against the additional asymmetry in steps 2 and 4. When you withdraw the liquidity in step 4 you get back a different mix of token X and Y than you put into the pool in step 2.

Maybe these two things would cancel each other out or even cause a net loss. Or perhaps, depending on the quantities involved, you sometimes got a profit and sometimes a loss. I needed to investigate this more closely.

To be clear upfront, I didn’t actually think this attack was going work. Uniswap V2 has been around for too long for someone — were it real — not to accidentally notice it.

Spoiler alert: the attack doesn’t work so you can stop reading now if you’re not interested in attacks that don’t work. But if you’re interested in seeing why, we’ll prove it with the help of a little algebra.

Defining our variables

In this and following sections I’ll using notation similar to that found in the book Automated Market Makers: A Practical Guide to Decentralized Exchanges and Cryptocurrency Trading. However, you can find similar presentations in many places on the web.

• Let $A$ and $B$ represent the quantities of token X and token Y, respectively, in the pool. We will use subscripts e.g. $A_0$, $A_1$, etc to show how these quantities evolve over time.
• Let $a$ and $b$ represent the amount of token X swapped/received and token Y received/swapped.
• Let $k$ be the percentage of token X that we initially buy using token Y. $0 < k < 1$
• Let $f$ be the percentage of the current liquidity that we add to the pool. $f = 1$ means that we add 100% of the current liquidity into the pool. $0 < f$

We will now derive an equation that depends only on the variables $k$ and $f$.

Let’s get started.

Uniswap V2 is a constant product AMM which means it obeys the constant product rule. Thus, if we swap $k$ percent of the initial balance of token X, $A_0$. From the pool’s perspective we have:

$$\begin{align*} (A_0 - kA_0)(B_0 + b_0) & = A_0B_0 \\ (1 - k)(A_0B_0 + A_0b_0) &= A_0B_0 \\ A_0b_0 &= {A_0B_0 \over 1 - k} - A_0B_0 \\ A_0b_0 &= {A_0B_0 - A_0B_0 + kA_0B_0 \over 1 - k} \\ &= {kA_0B_0 \over 1 - k} \\ b_0 &= {k \over 1 - k}B_0 \tag{0} \\ \end{align*}$$

Thus we paid ${k \over k - 1}B_0$ in token Y.

Now we calculate the new token quantities in the pool

$$\begin{align*} A_1 & = (1 - k)A_0 \tag{1}\\ B_1 &= B_0 + {k \over 1 - k}B_0 \\ &= \left( {1-k \over 1-k} + {k \over 1 - k} \right) B_0 \\ &= {1 \over 1 - k}B_0 \tag{2} \\ \end{align*}$$

We now begin step 2, adding $f$ times the existing liquidity to the pool. To simplify things we denominate the value of the pool in terms of token Y. We also assume that the market price of the tokens does not change during this process.

$$\begin{align*} poolValue &= {B_0 \over A_0}A_1 + B_1 \\ &= {B_0 \over A_0}(1-k)A_0 + {1 \over 1 - k}B_0 \tag{by (1) and (2)} \\ &= (1 - k)B_0 + {1 \over 1 - k}B_0 \\ &= {(1 - k)^2 + 1 \over 1 - k}B_0 \\ \end{align*}$$

Thus the cost of adding $f$ times this liquidity is

$$\begin{align*} cost &= {f(1 - k)^2 + f \over 1 - k}B_0 \tag{3} \\ \end{align*}$$

The pool now has more liquidity. Using equations $(1)$ and $(2) we have:

$$\begin{align*} A_2 & = (1 + f)A_1 & = (1 + f)(1 - k)A_0 \tag{4}\\ B_2 & = (1 + f)B_1 \\ & = {1 + f \over 1 - k}B_0 \tag{5} \end{align*}$$

We now enter step 3 of the process and sell the tokens we received in step 1. That is, we sell $kA_0$ of token X. Using the constant product rule again we get:

$$\begin{align*} b_2 &= {kA_0B_2 \over A_2 + kA_0} \\ &= {{k(1 + f)\over{1 - k}}A_0B_0} \over {(1 + f)(1 - k)A_0 + kA_0} \tag{by (4) and (5)} \\ &= {k \over 1 - k} \cdot {(1 + f)A_0B_0 \over {((1 + f - fk - k) + k})A_0} \\ &= {k(1 + f) \over (1-k)(1 + f - fk)}B_0 \tag{6} \end{align*}$$

The new quantities in the pool are now:

$$\begin{align*} A_3 &= A_2 + kA_0 \\ &= (1 + f)(1 - k)A_0 + kA_0 \\ &= (1 + f - fk)A_0 \tag{7}\\ B_3 &= B_2 - b_2 \\ &= {1 + f \over 1 - k}B_0 - {k(1 + f) \over (1-k)(1 + f - fk)}B_0 \tag{by (5)}\\ &= {1 + f \over 1 - k}({{1 - {k \over (1 + f -fk)}})}B_0 \\ &= {1 + f \over 1 - k}\cdot{1 + f - fk -k \over 1 + f - fk}B_0 \\ &= {{1 + f \over 1 - k}\cdot{(1 -k)(1 + f) \over 1 + f - fk}}B_0 \\ &= {(1 + f)^2 \over 1 + f - fk}B_0 \tag{8} \end{align*}$$

Now we perform step 4 and withdraw our liquidity which is $f \over {1 + f}$ of the total liquidity. What is the return?

$$\begin{align*} return &= {f \over 1 + f}{B_0 \over A_0}A_3 + B_3 \\ &= {f \over 1 + f} \left( {B_0 \over A_0}(1 + f - fk)A_0 + {(1 + f)^2 \over 1 + f - fk}B_0 \right) \tag{by (7) and (8)}\\ &= \left( {f(1 + f - fk) \over 1 + f} + {f(1 + f) \over 1 + f -fk} \right)B_0 \\ &= {f(1 + f - fk)^2 + f(1 + f)^2 \over (1 + f)(1 + f - fk)}B_0 \tag{9}\\ \end{align*}$$

Phew. We now have all the ingredients necessary to work out our profit (or lack thereof).

First we’ll work out our return on step 3 vs step 1 which is just $b_2 - b_0$.

$$\begin{align*} & b_2 - b_0 \\ =& {k(1 + f) \over (1-k)(1 + f - fk)}B_0 - {k \over 1 - k}B_0 \tag{by (0) and (6)}\\ =& {k \over 1 - k}{1 + f - (1 + f - fk) \over 1 + f - fk}B_0 \\ =& {fk^2 \over (1 - k)(1 + f -fk)}B_0 \tag{10} \end{align*}$$

Now we can work out the profit.

$$\begin{align*} profit &= (b_2 - b_0) + return - cost \\ &= {fk^2 \over (1 - k)(1 + f -fk)}B_0 + {f(1 + f - fk)^2 + f(1 + f)^2 \over (1 + f)(1 + f - fk)}B_0 - {f(1 - k)^2 + f \over 1 - k}B_0 \tag {by (3), (9) and (10)}\\ &= \left({fk^2 \over (1 - k)(1 + f -fk)} + {f(1 + f - fk)^2 + f(1 + f)^2 \over (1 + f)(1 + f - fk)} - {f(1 - k)^2 + f \over 1 - k}\right)B_0 \\ \end{align*}$$

This is pretty messy algebra and it took me forever to get it right. I was worried that I’d missed some obvious opportunities for simplification so I passed it through Symbolab hoping it would come with something neater. When it didn’t I just kept it the way it was.

What’s interesting about the definition of $profit$ is that it’s one giant multiple of $B_0$ the initial number of token Y in the pool. If this factor is greater than zero then we have a profit!

So I typed this enormous and unwieldy equation into GeoGebra’s 3D plot (substituting $x$ for $k$ and $y$ for $f$). I also restricted the value of $k$ and $f$ ($x$ and $y$) for which it was plotted.

It ended up looking like this in GeoGebra.

It produced the most beautiful plot.

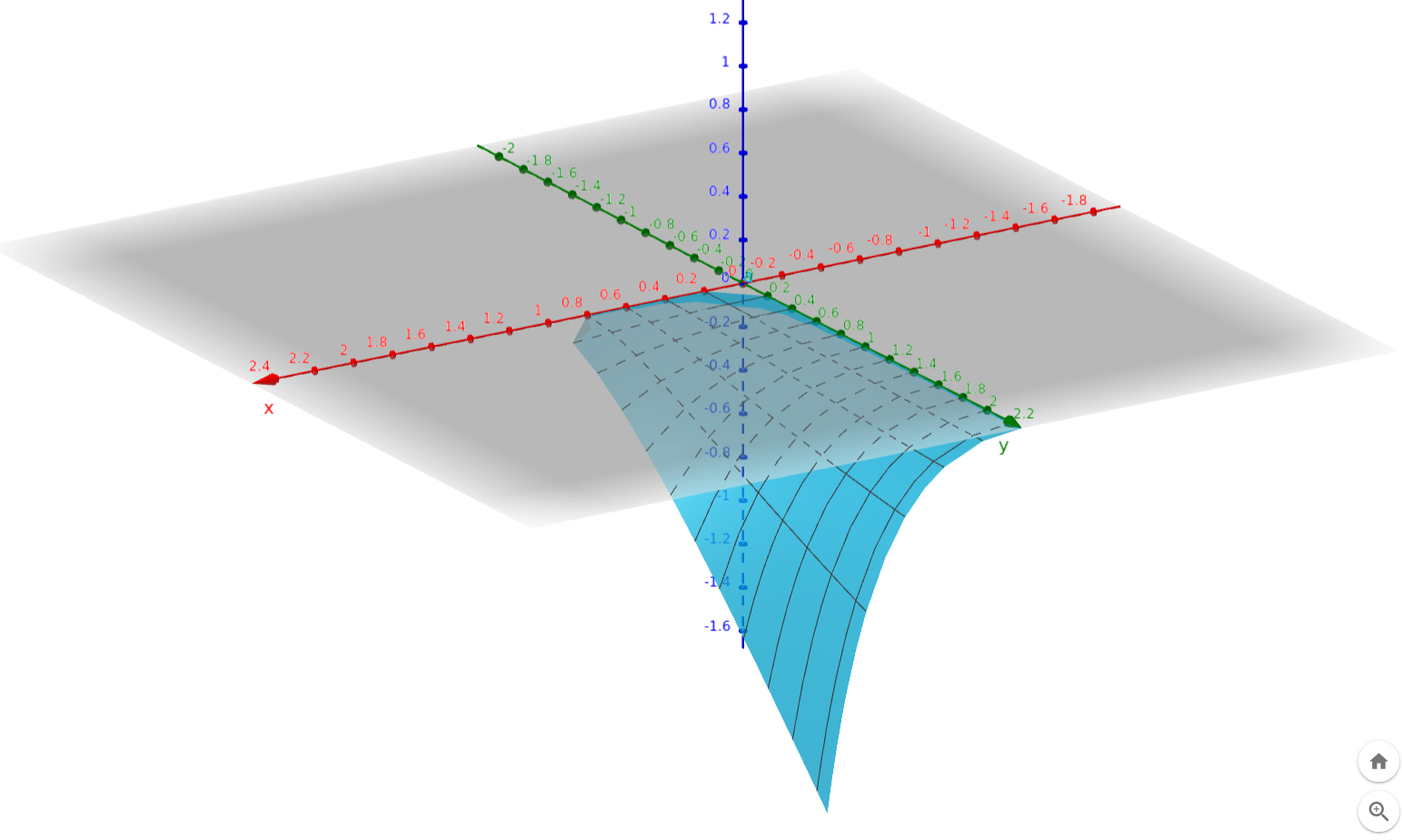
You can view and manipulate the plot here.

As you can see, at no point does the surface go above the $x$-$y$ plane. That is, there is no place in the range $0 < k < 1$ and $0 < f$ where its value is positive.

This proves that you can’t make any profit using this strategy.

In fact, as $k$ grows larger you make increasingly larger losses. The factor $f$ seems to act as an amplifier. If $k$ is fixed then the larger $f$ is, the larger the loss is.